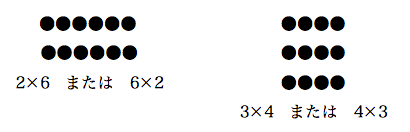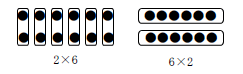立式の論理と計算の便宜 (3×5≠5×3問題)
1.
先月、ネットの片隅で盛り上がった話題に関連して。
以下に引用するyetanotherさんの主張は、学習指導要領解説を読み誤っている。いろいろ遠回りもするが、多くの言葉を費やして、その説明をしたい。
なお、話題の種となったもともとの問題について、結局のところ私自身が 3×5 と 5×3 のどちらを「よりよい答え」と考えるかについては、記事を分けた。結論はタイトルの通りである。→5×3 を推す(3×5≠5×3問題)(2010-12-21)
さて、あっさり結論から書いてしまうが、この指導要領解説中に乗法の式の順序を重視せよと書かれている部分は全くない。Kidsnoteで引用されている部分は「何を教えることが求められているか」についてであって、そこに乗法の式の順序が関係するとは全く書かれていない。
さらに以下の引用部分だが、
順序については、ここにばっちり出てます。
また,1 0×4 は,10 が4つあることから,40になると分かる。
この文章が登場するのはP.88「エ 簡単な場合の2位数と1位数との乗法 」の中であって、要するに10の位の数と1の位の数のかけ算についての話の中での文章であり、この件とは無関係である。
P.98には「D(2 ) 乗法の式 」という節があるが、式中の数字の順序については何も触れていない。
無いことの証明は難しいので、有ることの話をしよう。この指導要領解説で乗算の交換法則がどのように扱われているかだ。
P.81「エ 一つの数をほかの数の積としてみること 」には乗法の基礎となる積の概念を示す図がある。
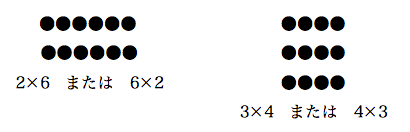
算数を教える教師にとって交換法則は自明なのにあえて「2×6 または 6×2」などと並記されていることに注目すべきである。
次にP.83にははっきりと「( 3) 内容の「A数と計算」の(2) のウについては,交換法則や結合法則を取り扱うものとする。 」とある。
さらにP.88の(さっきの10×4の例の次節に!)は「〔算数的活動〕(1) イ 乗法九九の表を構成したり観察したりして,計算の性質やきまりを見付ける活動 」として、児童に自然に交換法則に限らない数の性質について気がつくような指導を掲げている。この節の最後の文章は個人的には涙ものである。(強調は私)
乗法九九を構成したり観察したりす ることを通して,乗法九九の様々なきまりを見付けるように指導することは,児童が発見する楽しさを味わうことにつながるものである。
やれやれ。というわけで、指導方法としての「3×5≠5×3」の正当性を主張する方々は学習指導要領解説以外のところに典拠を求められるがよろしいと思う。
2.
まず、学習指導要領解説は、児童が学ぶ順番に沿って編集されているのではない。例えば、「第2学年の内容」から見出しを拾うと、以下の通りである。
2 第2学年の内容
〔A 数と計算〕
A(1) 数の意味や表し方
ア まとめて数えたり,分類して数えたりすること
イ 十進位取り記数法
ウ 数の相対的な大きさ
エ 一つの数をほかの数の積としてみること
オ 簡単な分数
A(2)加法,減法
ア 2位数の加法とその逆の減法
イ 簡単な場合の3位数などの加法,減法
ウ 加法,減法について成り立つ性質
A(3)乗法
ア 乗法が用いられる場合とその意味
イ 乗法に関して成り立つ性質
ウ 乗法九九
エ 簡単な場合の2位数と1位数との乗法
〔B 量と測定〕
(略)
〔C 図形〕
(略)
〔D 数量関係〕
D(1) 加法と減法の相互関係
D(2) 乗法の式
D(3) 簡単な表やグラフ
〔算数的活動〕
「A(1)数の意味や表し方」の中に加法、減法、乗法が登場し、その後「A(3)乗法」で乗法の基本的な説明が再び現れている。さらにずっと先に「D(2)乗法の式」がある。
何だこれは!? と面食らう方も多いだろう。簡単に解説すれば、小学2年生の算数で学ぶのは「数と計算」「量と測定」「図形」「数量関係」「算数的活動」であって、「足し算」「引き算」「掛け算」はそれらを構成する要素に過ぎない、ということだ。
しかし現実問題としては、まず掛け算を教えなくては「A(1) エ 一つの数をほかの数の積としてみること」を授業することは不可能であろう。学習指導要領解説は、「到達点」を示しているのであって、そこに至る「道のり」を詳述しない。それゆえ、教科書は1冊ずつ構成が異なっている。日本のあちこちで編集者らが知恵を絞り、もっとうまい構成はないか、こう教えたら成果が上がるのではないか、と熟議を重ねている。
ちなみに、10年ほど前の話だが、私も5種類ほどの教科書を比較検討したことがある。きちんと資料を残していないので、記憶で書くから話半分に読んでいただきたいが、乗法の学習は「A(3)ア→D(2)→A(3)イ→A(1)エ→A(3)ウ→A(3)エ→算数的活動」のような順序で教える本が多かったように思う。
まとめると、「乗算」という切り口で学習指導要領解説から内容を引き出す場合、学習指導要領解説の全体を読み、あちこちから記述を集め、再構成しなければならない。そして学習指導要領解説は、基本的に到達点を示しており、途中の指導に必要な便宜は、その少なからずを教科書や指導者の工夫に任せていることに、注意が必要だ。
3.
学習指導要領解説は基本的に、「**である」と説明し、「**ではない」とはいわない。これは簡潔をよしとする書類、重要度に応じて内容量の配分をすべき書類では標準的な記述法で、民間企業の作業標準書なども、多くは同様の形式でまとめられている。
通常、こうした書類の中に多くの人が誤解する部分などがある場合は、より信頼度の低い(その分、柔軟な対応が可能な)形で付属書や解説書を発行する。学習指導要領解説は、それ自体が学習指導要領の解説書なのだが、算数編などは200ページを超える大部だし、またこの解説の公的な重要度から考えるに、現在の編集方針は正しい。
誤解の多い箇所について「**ではない」という記述が必要であれば、学習指導要領解説の補足書を作成すべきだろう。民間企業の製品の仕様書や図面だって、標準、解説、補足の3段階くらい用意することは珍しくない。解説が膨大になるなら、補足の部分を切り分けて、解説書類もまた標準書類と同様の形式で作成するのは、実用の知恵である。
というわけで、学習指導要領解説のような文書を読み解くにあたり、「**が間違いだとは明記されていない」と言い募るのは悪手だ。その言い分が通ると、社会のあちこちで不都合が生じる。この場合は、「様々な記述に照らし合わせて、自然な解釈を採用する」という読み解き方を採用するのが妥当だ。
4.


掛け算が登場するのは2年生からだが、その基礎概念は1年生の段階から準備されている。例えば算数編のP64を参照してほしい。注目してほしいのは、「40は10の4個分」「10が6個で60になる」といった記述。「40は4個の10」「6個の10で60になる」とは書いていない。

単位量をまず示す、という解説の記述法は、P70に記載の意図にも合致している。

P76では加法の式の読み取りについて解説しているが、ここで解説者は「5+3=8」から「砂場で5人の子どもが遊んでいます。そこへ3人の子どもがきました。子どもは全部で8人になりました。」という物語を作っている。5+3 という数字の順番を無視してはいない。5がまずあって、そこに3を足す、と解釈している。

P77の例も同様である。

P63では繰り上がりの計算に必須となる、数の分解を扱っている。これは同時に、児童が加法の交換法則を帰納的に納得する仕掛けを示している。「交換法則」を道具として十全に活用するのは4年生からだが、1年生の段階で種はまかれている。
まあそれは余談で、ここで気付いてほしいのは、解説が 1+4 と 4+1 を異なる操作として列挙していることだ。もし 1+4 と 4+1 に何ら違いはないのだとすれば、1+4 と 2+3 の図のみ示せばよい。だが、そうはしていない。

解説書では、立式の論理と計算の都合とを区別している。P69の例題の状況を数式で表せば、8+7 となる。だが、そのままでは計算に不都合なので、数を操作するための便宜として、途中の式 (8+2)+5 や 5+(3+7) が登場するのである。(誤記修正 2011-02-01)
難しい箇所なので、落ち着いて読んでいただきたいのだが、数を操作する手段として登場する (8+2)+5 と 5+(3+7) は可換である。解説書の説明から、そう読み取れる。道具は自由に選べるわけだ。しかし、最初の式 8+7 は 7+8 と可換か? 「全く問題文の通りに立式する」という制約下では、非可換である。
学力到達度を測る試験において、7+8 という立式を誤答とするのは、正しい指導か否か。それは、わからない。学習指導要領解説は、そうした実践上の課題に答えを示してはいない。ただ、例題の状況を最も自然に表現した数式は 8+7 なので、「例えば」を付さずに 8+7 という式だけを示している。
8+7 でも 7+8 でもどちらでもよい、というのは、粗雑な考え方だ。数式は具体的な状況を要点を絞って表現するきわめて強力な手段である。計算して答えを得るための、一時的な道具ではない。数式は単体で意味を持っている。具体的な状況を言葉で詳述するよりも、数式によって端的に示す方が、本質をズバリ示すには好都合な場面は少なくない。
「太郎さんはどんぐりを8個拾ってきました。花子さんはどんぐりを7個拾ってきました。合わせて何個でしょう。」この問題文だけでは、太郎さんが先に登場する意味はわからない。意味はないかもしれない。しかし結果さえ正しければいいという立式は、「仕様通りに動作すればいいんだろう」というプログラムと同じで、第三者による検証や、よく似た他の事例への適用ができない。結果は最重要だが、大勢が思考の過程を理解できるよう、わかりやすい式を書き残すことも重要である。
計算上の意味が同じなら、式はどのように立ててもよい、と教えることには賛成できない。たしかに 8+7 と立式する方が自然だな、という感覚は育てた方がいい。が、その手段として、7+8 にバツをつけるというやり方がいいのかどうかは、別個に検討されてよい。問題は適切に切り分けてほしい。
補記:
これは 8+7 と 7+8 だから「どちらでもいい」気がするに過ぎないのであって、「計算結果が同じなのだから」という理屈を推し進めれば、最初から繰り上がりを考慮して 5+3+7 とか 5+(3+7) などと立式することも否定できない。一足飛びに 5+10 と立式するのはありやなしや?
交換法則だけは最初の立式から認めてよいという立場もあろう。だが、足し合わせる数が5つ以上にもなると、問題文通りではない式は、やはり意味不明に近付いていく。試験の採点基準は別として、理想形は 8+7 である、という指導はほしい。7+8 でもマルを与えるのはよいが、理想形を曖昧にすべきではない。
- まずは状況を素直に式で表現する。
- 式の結果を得る筋道は、自由に選択できる。
無論、理想形がひとつとは限らない。正解はひとつではない。高度に抽象化された、8+7 と 7+8 を「同じ」とみなせる状況を前提に考えを進めるべき場面も多々あるだろう。しかし、その事実からストレートに「P69の例だって 7+8 と表現してもいいじゃないか」という意見には与しない。
5.
乗法そのものは2年生で登場する。


いきなり核心に迫るが、P88の交換法則に関する記述をどう読むか。これを「自由に数字を交換して立式できる能力を育てようとしている」と解釈するのは早合点だ。解説は乗数と被乗数を区別し、A×B という式について、Aを被乗数、Bを乗数としている。乗法の初歩的理解に忠実な立式を心掛けるなら、逆はありえない。

P98-99は乗法の式の作り方、読み方を扱っている。式を作る例は正解の式を省略しているが、読み取りの例から類推すれば、「1袋に5個ずつ入ったみかんの4袋分」は 5×4 という式で表現されることがわかるだろう。もしこれを 4×5 と表現してもよいのだとすれば、3×4 という式から「プリンが4個ずつ入ったパックが3つあります」という物語を作ってもいいはずだ。しかし、学習指導要領解説の中に、そうした事例はない。

類推では不安だ、という方のために、P107の例を示す。これは3年生の内容の解説だが、「例えば,的当てで得点を競うゲームなどで,0点のところに3回入れば,0×3と表すことができる。3点のところに一度も入らなければ,3×0と表すことができる。」とある。学習指導要領解説が、初歩的な乗法の式における被乗数と乗数の並べ方をどう規定しているか、明快に理解されよう。

「被乗数×乗数」という順番が規定されていないとすると、P88の説明は意味不明である。
suzusukeさんは、批判を受けてP88からの引用を論拠から外してしまった。suzusukeさんは書きすぎた部分のみ訂正し、論拠の取り下げまではすべきでなかった。過剰反応もまた誤解を招く。
6.

yetanotherさんが、学習指導要領解説は 3×5 でも 5×3 でもどちらでもよいと書いている、と論じた根拠は、P81の「エ 一つの数をほかの数の積としてみること」の説明だった。
なるほどたしかに、2行6列の点の個数を数式で表す例について「2×6 または 6×2」、3行4列の点の個数を数式で表す例について「3×4 または 4×3」とある。だが、これは、被乗数と乗数のどちらを先に書いてもよいという意味ではない。そう読むと、他の記述と整合性が取れない。
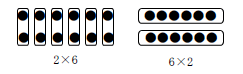
P81の例題は、被乗数と乗数を自分で定義するタイプの問題だ、と解釈するのが妥当だろう。
- 1列あたりの点の数を被乗数、何列あるかを乗数とすれば 2×6 となる
- 1行あたりの点の数を被乗数、何行あるかを乗数とすれば 6×2 となる
つまり、被乗数と乗数を自分で定義できる場合、2×6 と 6×2 が、ともに正しい式になりうる。しかしこの事実から「被乗数と乗数の順番など気にする意味はない」と結論することはできない。問題文中に1列あたりの点の数を被乗数とすることが明記されていれば、2×6 だけが正解になる。
Information
注意書き
- 筆者は徳保隆夫(とくほたかお)です。1980年愛知県生まれ。千葉県成田市育ち。メーカーに技術者として就職後、関東各地を転々としています。……という設定です。
- 私の文章は全て実記ではなく小説なので、客観的事実と異なる記述を多々含みます。
- 著作権は主張しません。詳細はInfoで、過去ログなどはNoteでご案内します。