

さらが5まいあります。1さらにりんごが3こずつのっています。りんごはぜんぶで何こあるでしょう。
個人的には、5×3 という式にバツがつくのはヘンだと思う。
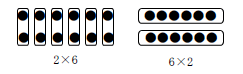
昨日の記事に登場した2行6列に並ぶ点の個数の問題に戻って考えてみよう。もし「1列ずつランプが点灯していって6列目でランプが全部点灯した」ということならば、2×6 と表現するのが自然だろう。だが、最初から2行6列の点があった場合、それは 2×6 でも 6×2 でもおかしくない。
初歩的な乗法のイメージにおいて、被乗数は固定量、乗数は変化量である(少なくとも学習指導要領解説は、まずそうした理解から乗法の学習をはじめることを想定している/そのことの是非は、今は問わない)。皿の枚数も、1皿あたりのリンゴの個数も固定量なら、どちらを被乗数にするかは、好きに選べばいい。「まず皿の数を数えて、次にそれぞれの皿に何個のリンゴがのっているかを考える」人と、「まず1皿あたりのリンゴの数を数えて、次に皿の枚数を数える」人、どちらもありえる。
文章には、書き手の行動や思考が反映されている。問題文は、まず皿の枚数に言及している。皿の上のリンゴの個数は、その次に書かれている。書き手は、まず皿の数を数えた、と想像できよう。とするならば、3×5 より 5×3 の方が自然ではないだろうか。
しかしながら、多くの人が、「5×3 が間違っているかどうかはともかくとして、3×5 の方が自然ではある」と考えた。さらには、5×3 という式を「被乗数と乗数を通常とは逆に書いた式」と解釈して、「そういう書き方をしたっていいじゃないか」といって擁護する人まで、何人も現れた。妙な話である。
つまるところ、文章を謙虚に読む人が少ないのであろう。
テーブルの上にリンゴの乗った皿が並んだ状況をリアルに想像してみれば、先に皿の数を調べるのは、とくに不自然な行動ではないと理解されるはずだ。先に皿の枚数が確定したので、これを被乗数とし、その時点で不確定な1皿あたりのリンゴの数を乗数とする。自然な思考の展開であろう。結果、皿は5枚、リンゴは1皿あたり3個だった。ならば、リンゴの個数は 5×3 である。
5×3 を間違いとはいわずとも、3×5 の方がより正しい、という側の根拠は何なのか。「1皿あたりのリンゴの数」という語感に引っ張られて、「1皿あたりの」の方が被乗数なんじゃないか? というコンセンサスが生まれ、なし崩し的に問題文それ自体よりも、多数派がその文章を読んで感じることの方が「正しい」ということになり、3×5 が正解だよね、となった……ということであろう。
混乱の原因は、「複数の皿にリンゴを1つずつ置く作業」を表現する適当な単位が日本語にないことである。
再び2行6列に並ぶ点の個数を計算で求める例を考えれば、もし日本語に「列」という言葉だけあって「行」という言葉がなかったならば、「1行あたりの点の個数」という日本語が成立せず、それゆえ、「1列あたりの点の個数」×「列数」という式だけが「自然」といわれたかもしれない。

上図は、「列」と「皿」、「行」と「全ての皿に1個ずつリンゴをのせること」を対応させたもの。この図を見てもなお疑問があれば、問題を除法に変換した次の例を見てほしい。
「皿の枚数」が単位量として自然に機能していることに注目していただきたい。
リボンを7本作ります。1本を8cmにすると、リボンは全部で何cmいるでしょう。
Benesseは「1つ分の数」は「リボン1本分の長さ」なので「8(cm)」、「いくつ分」は、「リボンの本数」なので「7(本分)」となり、かけ算の式は「8×7=56」となります
、と説明する。
問題文からは、「リボンを7本作ることが確定していて、長さの調整をしている」ことがハッキリ読み取れる。ならば、状況を最も適切に表現する数式は 7×8 だ。
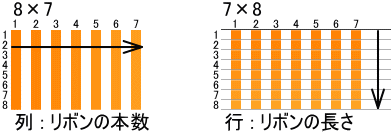
図解や除法の例から、リボンの長さと本数はどちらも「1つ分の数」になりうることがわかるだろう。この例が悲しいのは、Benesseの担当者が自分で例題を作成していることだ。自分の書いた文章の意味がわからず、片言節句にとらわれて、歪んだ式を立てる……。ところが、世間的には、Benesse派の人が多かろう。
算数も結局は国語力がないとダメだよね、なんていわれるけれども、私は国語が得意科目だったからこそ、算数の理不尽さには泣かされてきた。「大多数の人が誤読しているなら、誤読の方が正当な解釈となる」という理不尽は、国語の読解問題が本当に得意だった人なら、みな味わってきた悔しさではあるまいか。
そもそも論として、「被乗数×乗数」という順番が「自然」に思えるのは、日本語の性質による。英語圏では、英文法に従い乗数が先にくる。所詮、自然言語に依拠した話なので、高度に抽象的な議論をする場合、自然言語基準の「自然さ」は意味をなさない。
私はこの点について学習指導要領解説のような立場に賛成で、日本の小学生が学ぶ「算数」は、日本語となじむ形で教育するのが合理的だと考える。私は、そうした前提で書いている。
だがそのとき、国語の得意な人が直面する矛盾について書いだのが、この記事だ。「1皿あたりの」という言葉が出てくるや、多くの人が文章の読解を放棄し、無条件にこれを被乗数とする。国語の読解問題なら間違いとなる解釈が、多数決で「自然」とされ、3×5 を「最適な答え」へと押し上げる。
文章の「自然」な解釈とは、多数意見か、それとも実際に書かれている言葉そのものか。国語教育に慣れ親しんだ私は、後者だと思いたいわけだ。言葉と解釈が遊離してしまったら、言語による意思疎通など不可能であろう。ところが、算数の文章題指導は、大多数の人が同じ誤解をするなら、文章に書かれているままの意味とは関係なく、誤読を正解釈とする、というスタンスで行われている。
私は、悲しい。
国語の読解問題なら、クラスで1人しか書かなかった答えでも、正答は正答である。が、算数の立式では、大多数の人が問題文を読み誤るなら、その誤読に沿った式を書かねばならぬ。国語的に正しい解釈に沿って式を書いたら、バツになることさえある。これは国語の得意な人が直面する、国語科と算数科の指導方針の違いに由来する矛盾である。
国語科は、究極的により多くの人が共通の理解を持つためには、テキストに忠実に読む技術を養成せねばならぬ、と考える。算数科は、いますぐ教室の中に共通理解を形成しないと授業が進まないので、ある文章から大多数の人が想起するイメージがあるなら、それを正解釈ということにしたい。私は国語科の理想に共感するが、算数科の事情もわかる。
昨日の記事で、私は「問題文を適切に表現する式を書かねばならぬ。なぜなら数式は答えを得るための単なる通過点ではなく、それ自体がコミュニケーションの手段だからだ」と書いた(つもりだ)。とすると、Benesseの例のように、問題文を書いた当人が誤読準拠の式を正解とするのが現状なので、国語脳は封印するのが正解……なのか?
私も文章読解の勉強をやめて久しい。現在の私の読解力には疑いの目を向けてほしい。
問題文の筆者が、「さらが5まいあります。」を先に書いたのって、「引っ掛け問題」のつもりだったのかもしれないな。
記事を書き始めて数分後にその可能性に思い至り、脱力して半月くらい放り出していた。冒頭に「さらが5まいあります。」を配置した問題文が「引っ掛け問題」として成立しうるのは、「日本語の制約からくる先入観に基づく誤読が、逆に正当な読みとされる状況だから」だ。
盛り上がってるな、ということだけ把握して、その辺の記事はほとんど読まずに書いた。書き終えてから少し読んだら、私の書いたことの多くは、既に誰かが書いていた。いつものこととはいえ、今回は少し手間取ったこともあって、ゲンナリした。