注:「船が5艘あります。1艘に4人乗ります」という問題は『田中博史の算数授業のつくり方 (プレミアム講座ライブ)』p64が出典です。
私は「自分の発想で100%正解できる」のに、「先生の指導・誘導に従わないとバツがつく」ことに絶望していたのです。立式の形を制約しないと学校の先生が「この子はわかっている」「わかっていない」の区別がつかないとしても、それは教師側の問題。それを生徒の自由を縛って解決するのは、自分の無能のツケを生徒の絶望で支払う行為。許せない。
田中さんの本にあった問題文を図で表すワークは素晴らしい。図解によって児童の考え方を教師が把握できるならば、多様な立式を許容する指導も可能になります。ところが、田中さんには前述の「許せない」という感覚が薄いから、きちんと図を描けている子どもに単一の式を強要してしまう。本末転倒ではないか。指導上の都合で解法に制約を加えたのであって、本来は多様な解法が許容されるべき。指導上の都合が解消されているにもかかわらず制約を押し付け続けることに、いったい何の意味があるのか。
takehikomさんも、『トランプ配りは教育上有害』が典型的ですが、手段と目的が転倒しているように見えます。もし算数教育の関係者がみなtakehikomさんと同じような感覚なのであれば、成績上位層の子を絶望させない指導法など、100年待っても研究も発見もされそうにない。問題が「問題」と認識されてすらいないのですから。
どれも既に述べたことの繰り返しですね……。以下、気になる点へのレスポンスと補足など。
教師ではなく,教育システムでしょうね.この種の出題が1人の教員によるものではないことは,上の「B県学力調査」が示唆しています.
実際、そうなのでしょうが、生徒には関係ない話だと思います。私の場合は、年度末の実力テストでは解法自由で、そこでは思う存分やれたので、怒りは日々の授業を担当する教師に向きました。
平成23年6月17日の内容全体から,「指導は教員1人で行う」ことを暗黙の仮定としているように思われます.違っていたら,すみませんが補足をお願いします.
何のことだかわかりません。より具体的な指摘をください。例えば、もし私の文章がどのように書かれていたら、「指導は教員1人で行う」ことを暗黙の仮定として
はいないように読めるのでしょうか。そして、その仮定がなかったとしたら、私の主張はどのように変化するだろうとお考えなのです?
『「5艘」が基準量となりえない理由がない』と考えるとして,出題状況,それまでに学んだこと,そして5×4という立式からは,思考プロセスがまったく伝わりません.
それは教師の都合。生徒には関係ない。5艘の船があって、4人ずつ乗っているのだから、5×4で乗船者の総数がわかるに決まってます。なのに「まぐれ当たりをふるいにかけるため」なんて理由で、同種の問題を確実に解ける子が5×4とするのをバツにするのは馬鹿げてます。
教師が何を教えていようと、あるいは教えていなかろうと、5艘に4人ずつで5×4と考える子は出てくるし、それで絶対に総乗船者数を正確に求められるのだから、教師の都合でバツにするのはやめてほしい。
必要悪でしかないものを積極的に評価するのは間違っています。takehikomさんの挙げた例でいえば、救急医療の世界で現在「トリアージ」が必要だとしても、「トリアージが必要な状況は解消されるべき」という認識は共有されていて、できる限りトリアージをしないですむよう、みなが知恵を絞っていると思う。
翻って、「被乗数は1あたり量に限定する。4人/艘は1あたり量だが、5艘は違う」という指導をする人々は、そのような指導をせずにすむ道を本気で探してますか。その指導によって授業をつまらなく感じる子に対して、その犠牲が必要になる理由を明確に説明できるよう、実証データを集めようとしていますか。全てNoだと私は思う。「算数は得意だけど、算数の授業は大嫌い」な子どもが出てくるのは当然でしょう。
船の改装を持ち出すのは,作為的であり,不自然です*6.
私が5艘を基準量としたのは、問題文の中で船の数が先に確定しているから。5艘の船に4人ずつ乗るなら、5×4で総乗船者数がわかるね、と。これに対して、「5艘は基準量たりえず被乗数にはできない」という反論を予想したので、仮に被乗数=基準量という前提を受け入れたとしても、「5艘は基準量となりうるから被乗数にしていいんだよ」という思考実験を示したまでのこと。作為的であっても、「船の数は絶対に基準量たりえない」という命題に反例を示せたなら、用は足りています。
ケーキほかの問題については,過去の誤記に目を閉ざす者はの最初の図で,有向辺ではなく自由に行き来できるという考えを採ると理解しました.
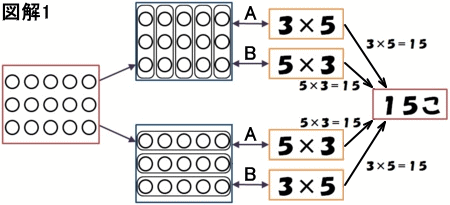
最初からグループ分けした図が示されている場合、A「丸を3つ内包するグループが5つある」と考えたなら3×5、B「5つのグループがあり、それぞれ3つの丸を内包している」と考えたなら5×3と式を立てて丸の総数を求めるのが自然だと思います。(*今にして思えば『5×3を推す』の2番目の図は暗黙の前提が隠れており説明不足)

式は書き手の状況認識を簡潔に表現したもの。図の読み方は1通りでないのだから、式も1通りではない。その点、文章は解釈の幅が狭いので、文章に忠実に立式すれば、式のバリエーションは限られます。
あと字面の話で申し訳ないのですが,平成23年6月17日という1日の中で,あるところでは「3個/皿」とper付きの単位を書き,また別のところで上のように「5艘」と書いているのは,読んでいて落ち着きません.
??? 3個/皿は3個/皿、5皿は5皿、4人/艘は4人/艘、5艘は5艘ですよね。
念のため。6月17日に書いた通り、「徳保的算数」を工夫なく扱った授業が、現在の標準的な指導法より優れているとは思っていません。私が受けたかった授業と、クラスの多数派にとって望ましい授業は違うでしょう。実証データは一度も目にしたことがありませんが、標準的な指導法の方が「掛け算がわかる」子の割合を高められるのだろう、と予想しています。実際に「徳保的算数」で授業するには、何らかのブレイクスルーが必要なのだろう、と思います。
そうではあっても、「掛け算のわからない子が減って、よかったね」と現状に満足されては困るのです。算数の苦手な子を救うためには「混乱のもと」を極力減らすのが定石であり、だから確実に正解を導ける考え方の多くを「算数の授業においてはバツ」と決めて正解の種類を大幅に減らした……その結果、授業に絶望し、教師を心底憎む生徒を生み出しているからです。小学校の先生方は、小学2年の標準的な掛け算指導法が、多くの子どもを救うために少数の子どもに犠牲を強いていることについて、もっと真剣に向き合ってほしい。
私が最近読んだ『わかる教え方 算数2年』『だれでもできる学力づくり2年』『田中博史の算数授業のつくり方』には、少なくとも小学2年の掛け算指導に関して、そうした逡巡が伺えない。「仕方なく特定の解法を押し付けることにした」という後ろめたさがない。今や手段が目的に摩り替わり、例えば「5艘の船に4人ずつ乗る場合の総乗船者数を求める際、5×4と計算するのは間違いだ」と断じて胸を張ってしまう。なぜ「残念ながら教育学は未だ5×4をバツにするより効果的な指導法を見出せていない」と悔しそうにしないのか。
5艘に4人ずつなら5×4、という発想で確実に正解できるのに、それをバツにして、いいことをしたような顔をしているから、小学校の教師は憎まれるのだと思う。医療リソースの不足に起因する命の選別に胸の痛みを感じない医療関係者はほとんどいないだろうに、どうして教師には鈍感な人が多いのか。