7 : 15 平方剰余の相互法則

前 7 - 14 p ｜ もくじ i ｜ 次 7 - 16 n

***と表示されるパスワードを読み取るツール

2003年 3月30日
記事ID d30330

小粒でもピリリと辛いフリーウェアシリーズ、今回は「パスワード読みとり」つながりで SnadBoy's Revelation v2。

DeFFFTPとして、FFFTPが暗号化して保存しているパスワードをデコードする方法を説明した。 「わざわざデコードしなくても通信を監視すれば良い」だの「みえみえ系を使えば良い」という考えもあるだろうが、 アルゴリズムを解析して暗号を自力で解読するというアプローチそれ自体に多くのかたは興味を感じると信じる。 しかし、DeFFFTPは、その名の通りFFFTPの暗号解除にしか使えない。 一般のパスワード（Windowsのエディットボックスで *** のように表示されるもの）を直接読み取るツールを紹介する。

名前は Revelation 、SnadBoy Software からダウンロードできる。 2003年3月現在バージョン2.0。

使い方は「みえみえパスワード」系の標準で、起動した画面にある円形のカーソル を、 見たいエディットボックスの上にドラッグすれば良い。

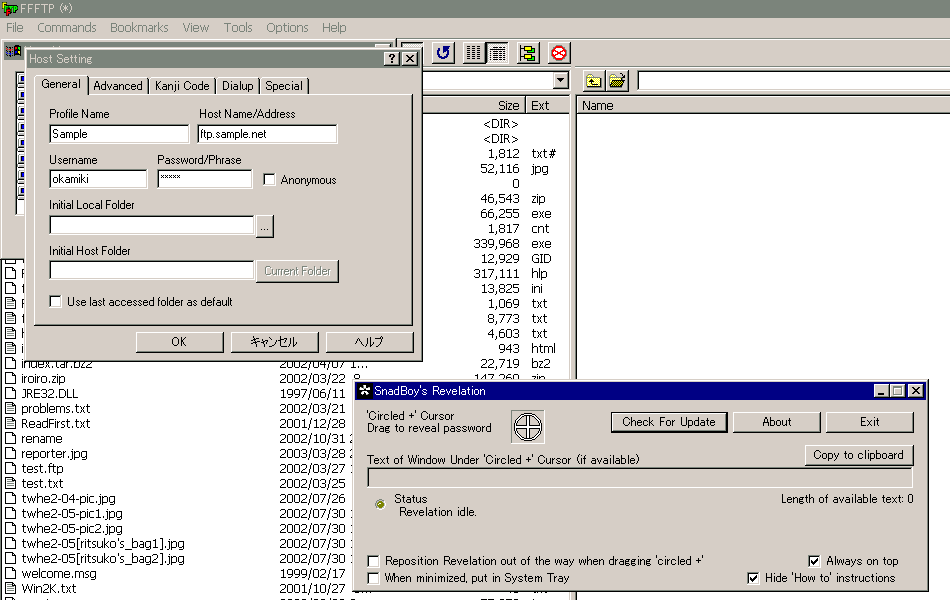
*** と隠されているパスワードが読み取れると、ソフト画面内に表示される。

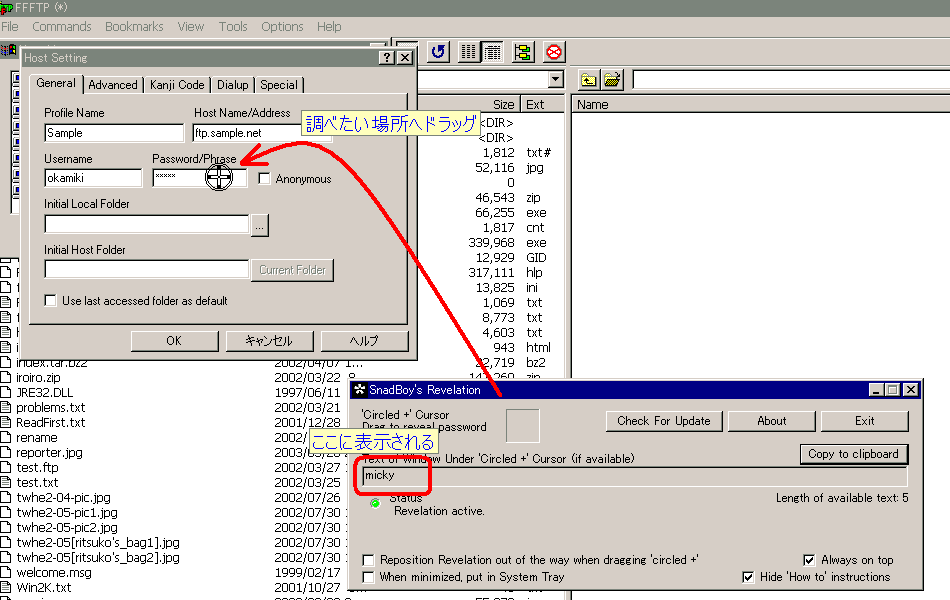
Windows 2000 で動作確認した。このツールは起動するとネットと通信しようとするが、通信を許可しなくても動作する。

リンク

関連記事

• DeFFFTP (2003-03-25)

  FFFTPに保存したログインパスワードを忘れてしまったとき復元

ほかの小粒ツールより

• そのJPG、ムダに大きくありません？ (2002-01-09)

  ゴミヘッダを除去して画質には全く影響を与えずJPGを5KBぐらい小さくするツール

参考

• みえみえパスワード: エディットボックスで *** のように表示されているパスワードを見るツール。Win 2000 / XP では使えない。
• CenriGun - 千里眼 同様のツール。XP対応をうたっているが見れないパスワードも多いようだ。

この記事のURL

• http://www.fairyland.to/articles/7/15/#d30330
• http://www.faireal.net/articles/7/15/#d30330

｜テキスト版｜省パケ版｜XML版｜

平方剰余（へいほうじょうよ）の相互法則

2003年 3月26日
記事ID d30326

平方剰余（へいほうじょうよ）というのは難しそうな名前だが、 早い話が「平方数」のことだ。 ふつうの整数で 4, 9, 16, 25, ... などは平方数（ある整数の二乗）だが、3, 6, 14, 23 などは平方数でない（ある整数の二乗にならない）。

7を法とする世界で考えよう。7を法とすると、
0² = 0 ≡ 0
1² = 1 ≡ 1
2² = 4 ≡ 4
3² = 9 ≡ 2 （9を7で割ると2余る）
4² = 16 ≡ 2 （16を7で割ると2余る）
5² = 25 ≡ 4 （25を7で割ると4余る）
6² = 36 ≡ 1 （36を7で割ると1余る）
となっているので、この世界では、0, 1, 2, 4 が平方数だ。 また、3, 5, 6 は平方数でない。「7を法とする平方数」「7を法とする平方数でない数」のことを、 「7の平方剰余」「7の平方非剰余」というのだが、言葉遣いが難しいと分かりにくくなるので、ここでは「平方数」で通す。

以下で説明する平方剰余の相互法則は、古典的整数論においては「基本」であると同時に「数の神秘」であり、ひとつの山場ともなっている。 イデアル論の立場からは別に神秘的でなく透明に理解することができるので、二次体を導入してから平方剰余の相互法則に進むのが現代的かもしれない。 しかし、平方剰余の相互法則の意味そのものは中学生にも理解できる。 巨大素数を扱う暗号学の立場からは、相互法則はヤコビ記号を使うソロベイ・ストラッセン・テストの基礎となっている。 確率的素数判定であるから、このテストをすりぬける「オイラー擬素数」の概念も生じる。

RSA暗号系から派生したネタとして、 フェルマーの小定理と擬素数、ラビン・ミラーのテストと強擬素数についてすでに書いた。 これらは暗号システムそのものというより「どうやって暗号に使う巨大素数を用意するのか」という下準備のような話だった。 話のついでなので、擬素数つながりで、ソロベイ・ストラッセン・テストとオイラー擬素数にもふれよう。 そのため、今回は平方剰余の相互法則を導入しておく。次回ルジャンドル記号とヤコビ記号を導入してオイラー擬素数まで行く予定だ。 なお、ここでは具体例の観察だけで証明はつけないので、詳しくは将来、自分で勉強してほしい。

ある数が平方数であるかないか

上でみたように、7を法とすると、0, 1, 2, 4 は平方数、3, 5, 6 は平方数でない。このことを次のように略記しよう:
0 R 7
1 R 7
2 R 7
4 R 7
3 N 7
5 N 7
6 N 7

a R b とは x²≡a (mod b) を満たす x が存在するということであり、 a N b とは x²≡a (mod b) に解がないことを言っている。

問題: 17 R 13 か？

解答: はい。mod 13 では 17≡4 だから x²≡4 (mod 13) に解があるか考える。2を二乗すれば4なので解がある。2² = 4 ≡17 (mod 13)

問題: 13 R 17 か？

解答: はい。8² = 64 ≡ 13 (mod 17)（64を17で割ると3余り13なので）

第一の例から分かるように、13を法として4が平方数か？ということと17が平方数か？ということは、同じ意味になる。 4≡17 (mod 13) だからだ。つまりＡが平方数かどうか？と尋ねているとき、実際にはＡという特定の数について尋ねているというより、 Ａと合同なすべて剰余類について尋ねていてＡという数はその代表例にすぎない、と考えても良い。 だから厳密な用語としては「平方数」（数）でなくて、その数をひとつの代表例とするような「平方剰余」（剰余類）ということになる。 この区別は言葉の上の話で、あまり本質的でないので、分からなければ気にしなくて良い。

問題: 6は17を法として平方数か？　言い換えれば 6 R 17 か、それとも 6 N 17 か？

ちからまかせにやるには、全部の可能性をかたっぱしからチェックすれば良い。
0² ≡0
1² ≡1
2² ≡4
3² ≡9
4² ≡16
5² ≡8
6² ≡2
7² ≡15
8² ≡13
9² ≡13
10² ≡15
11² ≡2
12² ≡8
13² ≡16
14² ≡9
15² ≡4
16² ≡1
……17を法とする世界では何を平方しても6にはならないことが分かる。したがって答は「いいえ」だ。6 N 17 である。

ところで、さらによく観察すると、この場合、1の平方と16の平方は等しく、2の平方と15の平方は等しく……以下同様に、 nの平方と17-nの平方は等しくなっている。これは当たり前のことで、
(17-n)² = 17² - 2·17·n + n² ……①
の右辺第一項、第二項は17で割り切れるので、17で割った余りという観点ではこれらは0に等しく、
(17-n)² ≡ n² (mod 17)
だからだ。ということは、1の二乗、2の二乗……と計算していくと、半分の17/2より先には新しいものはでない。 言い換えれば、上の計算結果では、0は別にして、右辺には同じ数がぜんぶ2回ずつ現れる。 したがって、17を法とする世界では、すべての元が平方数ということは不可能で、0を除外した16個の要素のうち半分が平方数、 残りの半分が非平方数だ。実際、上の結果から、0は別にして、1, 2, 4, 8, 9, 13, 15, 16 の8個が平方数である。 法が7でなくても①と同様の式は成り立つので、かたっぱしから調べるにしても法の半分までで止めて良い。

ここで、与えられた整数 a が b を法として平方数になるかならないか、ちからまかせに調べる関数をとりあえず作っておく。

function test( a, b ) {
    a %= b;
    for( var i=0; i <= b/2; i++ ) {
        if( i*i % b === a ) return "R";
    }
    return "N";
}

この関数は、与えられた２数 a, b について、a R b なら "R" を返し、 a N b なら "N" を返す。

交換法則が成り立つか

与えられた2つの数 a, b が、a R b であるか a N b であるか。 つまり、a は平方数 (mod b) であるかどうか。 あとから説明するように、a, b はともに3以上の素数と仮定して良い。 それ以外の場合も、3以上の素数の計算に帰着させられるからだ。

a, b を3以上の素数として、a R b なのか a N b なのか一覧表を作ってみよう。 とりあえず20未満の範囲で実行する。

var Primes = [ 3, 5, 7, 11, 13, 17, 19 ];

d.write("<table>");
for( var i = 0; i < Primes.length; i++ ) {
    var a = Primes[i];
    d.write("<tr>");
    for( var j = 0; j < Primes.length; j++ ) {
        var b = Primes[j];
        if(test(a,b)=="R") d.write( "<td style='background:#cff'>" + a + "R" + b + "</td>");
        else d.write( "<td style='background:#fcc'>" + a + "N" + b + "</td>");
    }
    d.write("<\/tr>\n");
}
d.write("<\/table>");

この表を観察すると、左上から右下への対角線にそって、だいたい対称になっている。 a R b なら b R a 、a N b なら b N a であることが多いようだが、多少、例外もある。 この問題をハッキリさせるため、次の形式で表を出力してみる。

var Primes = [ 3, 5, 7, 11, 13, 17, 19 ];

d.write("<table>");
for( var i = 0; i < Primes.length; i++ ) {
    var a = Primes[i];
    for( var j = 0; j < i; j++ ) {
        d.write("<tr>");
        var b = Primes[j];
        if(test(a,b)=="R") d.write( "<td style='background:#cff'>" + a + "R" + b + "</td>");
        else d.write( "<td style='background:#fcc'>" + a + "N" + b + "</td>");

        if(test(b,a)=="R") d.write( "<td style='background:#cff'>" + b + "R" + a + "</td>");
        else d.write( "<td style='background:#fcc'>" + b + "N" + a + "</td>");

        d.write("<\/tr>\n");
    }
}
d.write("<\/table>");

(7, 3), (11, 7), (19, 3), (19, 7), (19, 11) の組み合わせでは、 式の２つの数字を入れ替えると R か N か？の性質が変わる。 これらの数が入っていても、(7, 5) や (13, 7) は問題なく交換できている。 同じ素数でも、5, 13, 17 が入っている場合は交換法則が成り立ち、3, 7, 11, 19 同士では成り立たない。 いま、5, 13, 17 を「バニラ素数」と呼び、 3, 7, 11, 19 を「チョコレート素数」と呼ぶと、

• バニラ同士は交換できる
• バニラとチョコレートも交換できる
• チョコレート同士は交換できない

交換できない、といっても、では予想がつかない結果になるのか？というと、そうではなく、 ここで「交換できない」という意味は、a R b なら b N a になり、a N b なら b R a になるということ、 つまり R と N が正確に入れ替わることを意味している。

4で割って1余る素数、4で割って3余る素数

5, 13, 17, ... のような「バニラ素数」の正体は、4で割って1余る素数であり、 3, 7, 11, 19, ... の「チョコレート素数」は4で割って3余る素数だ。 （素数なので4で割れば必ず余りが出る。2を除外して奇数を考えているので、4で割って2余ることはなく、必ず1か3余る。） 目で見て分かりやすくするために、バニラ素数とチョコレート素数を区別して表示させてみよう。

var d = document;
function display( a, b ) {
    var test1 = test( a, b );
    var test2 = test( b, a );
    var A = flavor( a );
    var B = flavor( b );

    if( test1 === "R" ) {
        d.write('<td style="background:#cff">' + A + 'R' + B + '<\/td>');
    } else {
        d.write('<td style="background:#fcc">' + A + 'N' + B + '<\/td>');
    }

    if( test2 === "R" ) {
        d.write('<td style="background:#cff">' + B + 'R' + A + '<\/td>');
    } else {
        d.write('<td style="background:#fcc">' + B + 'N' + A + '<\/td>');
    }

    if( test1 === test2 ) {
        d.write('<td style="background:#fff; color:green">入れ替えても同じ<\/td>');
    } else {
        d.write('<td style="background:#ffd; color:red; font-weight:bold">入れ替えると逆転<\/td>');
    }

    if( a % 4 === 1 || b % 4 === 1 ) {
        d.write('<td style="background:#fff; color:blue">バニラを含む<\/td>');
    } else {
        d.write('<td style="background:#ffd; color:maroon; font-weight:bold">チョコレート同士<\/td>');
    }
}
function flavor( n ) {
    if( n % 4 === 1 ) return '<em style="color:blue; background:white">' + n + '<\/em>';
    else return '<strong style="color:maroon">' + n + '<\/strong>';
}

var Primes = [ 3, 5, 7, 11, 13, 17, 19, 23, 29 ];

d.write('<table>');
d.write('<tr><th>元の式<\/th><th>入れ替えた式<\/th><th>R か N か<\/th><th>式の内容<\/th><\/tr>\n');
for( var i = 0; i < Primes.length; i++ ) {
    var a = Primes[i];
    for( var j = 0; j < i; j++ ) {
        d.write("<tr>");
        var b = Primes[j];
        display( a, b );
        d.write("<\/tr>\n");
    }
}
d.write("<\/table>");

バニラ素数同士や、バニラ素数とチョコレート素数は、ひっくり返しにしても R ないし N の性質は変わらないが、 チョコレート素数同士の場合、ひっくり返しにすると R だったものは N に、N だったものは R に変わる。 以上が「平方剰余の相互法則」の内容だ。

今回のまとめ

例題

x² ≡ 3 (mod 23977) …… ① には解があるか？

答: 3はチョコレート素数だが、もう一方の数23977は4で割ると1余り、バニラ味だ。 したがってひっくり返しても判定結果は変わらない。
x² ≡ 23977 (mod 3) …… ② には解があるか？

23977≡1 (mod 3) だから、要するに
x² ≡ 1 (mod 3) には解があるか？
と尋ねている。ということは ② には x = 1 という解があるので、①にも解がある。

ちなみに、①の具体的な解は 6033であり、6033² = 36397089 を 23977 で割ると3余る。 ソロベイ・ストラッセン・テストによる素数性判定では、①の形の式を実際に解く必要はなく、単に解があるかないかだけ知りたい。 したがって泥臭い数値計算をする必要はなく、今回説明した平方剰余の相互法則と、次回以降に説明するヤコビ記号の性質によって、 高速に判定を実行できる。 なお、両方とも4で割って3余る形の数でも、 計算上、支障はない。 その場合、ひっくり返すと平方数か平方数でないか？の性質が入れ替わる。

この記事のURL

• http://www.fairyland.to/articles/7/15/#d30326
• http://www.faireal.net/articles/7/15/#d30326

｜テキスト版｜省パケ版｜XML版｜

前 7 - 14 p ｜ もくじ i ｜ 次 7 - 16 n