「4つの4で遊ぼうよ」シリーズの式検索は、充分に網羅的でないし、必ずしも効率的でなかった。当初の方法からみれば相当に高速化した「ラムダ関数バージョン」ですら、まったくムダが多い。4つの4を使って作れる数全体を調べるときに、評価される値を数え上げるのが目的であるにもかかわらず、構成可能なすべての表現を数えてしまっているからだ。詳しい説明は省くが、以下のようなまったく異なる発想を用いることが望ましいように思われる。
oValueToExpression という型のオブジェクトを考える。実質的には、値(数式の「意味」)をキーとしてその値をもたらす表現(数式、命令)を値とするハッシュである。
出発要素 var EVE = [ "4" , 4 ] ひとつの記号 "4" と、その記号の意味である数値 4 の対である。oValueToExpression1 に属するキーは、これだけだ。つまり、4という値をキーとして、"4" という文字列をひきだすハッシュ。
oValueToExpression1 を豊かにするために有限個の一項演算子μ∈MONO を適用する。ここでは、「何もしない」「平方根をとる」「階乗を返す」の3種類の一項演算子だけを考え、すべての項は(必ずしも相異ならない)一項演算子を3重にとることができるものとする。
function enrich( Seed , oValueToExpression ) {
var expression;
for(var i=0; i< MONO.length-1; i++) {
for(var j=0; j< MONO.length-1; j++) {
for(var k=0; k< MONO.length-1; k++) {
var value = MONO[k](MONO[j](MONO[i]( Seed[1] )));
var param = "1" + i + "" + j + "" + k;
var expression = "Func" + param + "( " + Seed[0] + " )";
if( oValueToExpression[ value ] === void 0 ) {
oValueToExpression[ value ] = expression;
}
}
}
}
}
MONOは、1変数関数の配列である。Seed はハッシュでoValueToExpressionの全範囲を走る。Seed[0] が記号、Seed[1] がその記号を解釈したときの値。
oValueToExpression1をこの関数で豊かにしてoValueToExpression1Exを得る。次に加減乗除の4つの二項演算子OP2からなる集合を考える。この段階では我々が知っている一項はoValueToExpression1に尽きるので、それと自分自身の直積を走る。
for( value1 in oValueToExpression1Ex ) {
for( value2 in oValueToExpression1Ex ) {
for( var i=0; i<OP2.length; i++ ) {
var value = OP2[i]( value1, value2 );
if( oValueToExpression2[ value ] === void 0 ) {
var expr1 = oValueToExpression1Ex[ value1 ];
var expr2 = oValueToExpression1Ex[ value2 ];
var expression = "OP2[" + i + "](" + expr1 + "," + expr2 + ")";
oValueToExpression2[ value ] = expression;
}
}
}
}
if( oValueToExpression[ value ] === void 0 ) は重要だ。すでにオブジェクトが valueプロパティを持っているなら、そのvalueの作り方をオブジェクトは「知っている」。valueプロパティの値がそのvalueを構成する式を表す文字列だからだ。これまで表現中心にすべての表現を数え上げようとしていたが、今度は意味中心に考え、すでに作り方を知っている要素は原則的に無視する。例えば、4+4+4 で12が作れることを知っているなら、4+(4+4) を含む表現はいっさい考える必要がない。また、4/(4-4) がゼロ除算で無効であることは3項式の段階で判明するから
4+4/(4-4) , 4/(4-4)*SQRT(4) , ...
といった4項式を個別に評価するのは時間のムダでしかない。最初から4項あるとして表現空間を捜索せずに、小さい方向から徐々にナンセンスでないものを構成していけば良い。
こうして我々はoValueToExpression2を得た。これは2つの4を使って作ることのできるすべての数の集合、のようなもので、しかも、それらの数はレシピがハッキリしている。例えば、16の作り方は、文字列"16"をキーとした
oValueToExpression2["16"]
に入っている。たぶん OP[2](Func1000(4), Func1000(4)) というレシピであろう。OP[2] は2変数関数MULへの参照、Func1000 は何もしない単項演算子。
次に、oValueToExpression2を一項演算子で豊かにしてoValueToExpression2Exを得る。これとoValueToExpression1Exの直積にまったく同様に二項演算子を適用してoValueToExpression3を得る。この場合、1Exと2Exをこの順序でかけるのと、さかさの順序でかけるのとで生成空間が異なるのでべつべつに数える。もちろん右からかけたときにすでにレシピがあるモノは左からかけて出現しても無視して良い。
oValueToExpression3を豊かにした3Exには、3つの4を使って生成できるすべてが含まれる。あとは、1Ex×2Ex、2Ex×2Ex、3Ex×1Exを調べて、和集合をとればoValueToExpression4が得られ、それを豊かにしたものは、4つの4で作れるすべてを過不足なく含む。最初から4項を含む表現を機械的に網羅、列挙してそのすべてをひとつずつ評価する方法は効率が悪い。
実際、当初は0~100を調べあげるのに何分もかかっていた。そのごの改善もあったが、10秒くらいはかかっていた。上の発想を使えば、0~1000(100でなくて千)の範囲を1秒未満でスキャンできてしまう。
ただし、ここでは総和記号(整数 n に対して n(n-1)/2 を返す一項演算子)を用いていないから、検索する表現空間が異なる。他方において、従来のアルゴリズムでは検索対象外だった2項演算の結果に1項演算をほどこすたぐいも検索対象になっている。
以下は出力例。
0 == SUB(( 4 ),( - ( SUB(( 4 ),( ADD(( 4 ),( 4 )) )) ) ) ) 1 == DIV(( 4 ),( - ( SUB(( 4 ),( ADD(( 4 ),( 4 )) )) ) ) ) 2 == SUB(( 4 ),SQRT( MUL(( 4 ),( DIV(( 4 ),( 4 )) )) )) 3 == SUB(( 4 ),( DIV(( 4 ),SQRT( MUL(( 4 ),( 4 )) )) )) 4 == MUL(( 4 ),( DIV(( 4 ),SQRT( MUL(( 4 ),( 4 )) )) )) 5 == ADD(( 4 ),( DIV(( 4 ),SQRT( MUL(( 4 ),( 4 )) )) )) 6 == ADD(( 4 ),SQRT( MUL(( 4 ),( DIV(( 4 ),( 4 )) )) )) 7 == ADD(( 4 ),( SUB(( 4 ),( DIV(( 4 ),( 4 )) )) )) 8 == ADD(( 4 ),( - ( SUB(( 4 ),( ADD(( 4 ),( 4 )) )) ) ) ) 9 == ADD(( 4 ),( ADD(( 4 ),( DIV(( 4 ),( 4 )) )) )) 10 == ADD(( 4 ),FACT( SUB(( 4 ),( DIV(( 4 ),( 4 )) )) ))
JavaScriptで直接解釈できる(人間が読みやすい)式を文字列で作ってそれを評価するかわりに、たったひとつの出発元 (4) から上向きに、どのような道筋で生成されるのか、という考えの表記法になっている。「通常」の表現との変換は、しかしながら、表面的な問題にすぎない。
上記の方法は、4つの4以外の4つの任意数ないし任意数の任意数のパズルにも、そのまま適用できる。とくに、任意の一項演算子、二項演算子の有限集合に対して、きわめてわずかの変更のみで、同じ解法が適用できる。一般フォーフォーズ問題は、「数の集合と演算子の対(演算子の使用方法について条件があっても良い)を生成者として、生成可能なすべての要素(その範囲に条件があっても良い)を枚挙せよ」、という型の問題であると定義でき、上記のように解くことができる。
「4つの4で遊ぼうよ」シリーズがアルゴリズム的には、ほぼ最終的な解決をみました。
デモ: http://m17n.cool.ne.jp/demo/four4s/four4s_1000_fastest/
4つの4を使って、0, 1, 2, 3, ... を表す式を作りなさい。
例
0 = 44-44
1 = 44/44
2 = 4-((4+4)/4)
3 = (4+4+4)/4
4 = 4+4×(4-4)
5 = (4+(4×4))/4
6 = 4+((4+4)/4)
7 = (44/4)-4
8 = 4+4+4-4
9 = 4+4+(4/4)
10 = (44-4)/4
10までは小学校の算数の計算でできますね。12, 15, 16もいけます。
12 = (4+44)/4
15 = 4+(44/4)
16 = 4+4+4+4
11, 13, 14 などは、どうでしょう? 小学校の算数ではできませんが、平方根を使えばできます。
11 = 44/(√( 4×4 ))
13 = (√( 4 ))+(44/4)
14 = 4+4+4+(√( 4 ))
17 = (4×4)+(4/4)
18 = 4+((4×4)-(√( 4 )))
ところが、19は、平方根まで使っても作れません。たす、ひく、かける、わる、と平方根だけでは作れない数は、40以下の範囲だけでも、19, 27, 29, 31, 33, 35, 39 があります。そこで、
1! = 1
2! = 2×1 = 2
3! = 3×2×1 = 6
4! = 4×3×2×1 = 24
5! = 5×4×3×2×1 = 120
6! = 6×5×4×3×2×1 = 720
7! = 7×6×5×4×3×2×1 = 5040
...
こんな感じです。この先は、驚くほど急激にどんどん大きくなります。例えば、
30! = 2 6525 2859 8121 9105 8636 3084 8000 0000
てな感じで、万、億、兆、
「4つの4」に話を戻して、平方根まででは作れなかった19なども、階乗までゆるせばこのとおり:
19 = ( 4! )-(4+(4/4))
20 = 4×(4+(4/4))
21 = (44-(√( 4 )))/(√( 4 ))
22 = 4+((√( 4 ))+(4×4))
23 = ((√( 4 ))+44)/(√( 4 ))
24 = 4+(4+(4×4))
25 = ( 4+(4/4) )√4
26 = 4+(44/(√( 4 )))
27 = 4+( 4! )-(4/4))
28 = 44-(4×4)
29 = 4+( 4! )+(4/4))
30 = (4×(4+4))-(√( 4 ))
31 = ( 4! )+((4+( 4! ))/4)
32 = (4×4)+(4×4)
25は、4+(4/4) の √4乗 として表されてます。5の2乗ってことですね。ほかにも作り方はあるでしょうが、この方法がいちばんシンプルでしょう。
さて、ここまで楽しくやってきましたが、33は階乗までゆるしても作れません。0~1000の範囲で、4つの4に
162 = [ √√√4 + √( 4×√√4 )]4
の場合は――四則、累乗、平方根、階乗の範囲では――上のように三重根号を認めて、初めて到達できるのです(この例の詳細については後述)。そんな複雑な可能性まで考慮しても、33は作れません。その先は、というと……
34 = (√( 4 ))+(4×(4+4))
35 = ( 4! )+(44/4)
36 = 44-(4+4)
37 = ( 4! )+ [ ((√( 4 )+( 4! )) / (√( 4 )) ]
38 = 44-(4+(√( 4 )))
までは良いとして、39も作れないのです。
ところで41は、ちょっとした驚異です。
40 = 4×(4+4+√( 4 ))
41 = √[ { (4!) + ((4+4)!) } / (4!) ]
ちょっと分かりにくいですが、4! と 8! を足して、和を 4! で割って、その全体の平方根をとるのです。
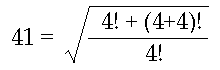
4! = 24, 8! = 40320 ですから、和は 40344、それを 4! = 24 で割ると 1681 で、確かに41の自乗になっています。
よくこんなの思いついたな、ですって? たぶん人間さんには思いつけないかもしれません…… 人間でなく JavaScriptが生成したものです。さらに進むと
42 = (√( 4 ))+44-4
43 = 44-(4/4)
44 = 4+44-4
45 = 44+(4/4)
46 = 4+44-(√( 4 ))
47 = ((√( 4 ))×( 4! ))-(4/4)
48 = 4×(4+4+4)
49 = (4/4)+((√( 4 ))×( 4! ))
50 = 4+√( 4 )+44
このように進めるのに、33と39が作れないのを放っておくのは気持ちが悪いので、なんとかしましょう。階乗(1からその数までの積)を許したのだから、総和(1からその数までの和)も許すことにしましょう。ここでは総和記号をΣ(シグマ)で表します。
Σ1 = 1
Σ2 = 1+2 = 3
Σ3 = 1+2+3 = 6
Σ4 = 1+2+3+4 = 10
Σ5 = 1+2+3+4+5 = 15
Σ6 = 1+2+3+4+5+6 = 21
...
「厳密」に言うと、例えば Σ4 は ![]() の略記法と考えることができます。もしくは、Σは n(n+1)/2 を返す
の略記法と考えることができます。もしくは、Σは n(n+1)/2 を返す
総和記号を使うと、問題の 33 , 39 も作ることができます。
33 = ((Σ( 4×4 ))-4)/4
Σ16 = 1+2+3+ ... +16 = 136 です。そこから 4 を引くと 132 、4 で割ると、たしかに 33 になります。39のほうはシンプル:
39 = (4×(Σ4))-(4/4)
総和記号もゆるすと、0から1000まですべて作ることができます。ただし、平方根、階乗、総和の単項演算子を各項ごとに一回だけに制限した場合には、この範囲で作ることのできる数は829個ほどです。
Σ(√(4)) = Σ2 = 3
Σ(Σ4) = Σ10 = 55
のように同じ項に対して特殊記号をいっぺんに二重以上に使うのを禁止した場合……ということです。この制限で作れなくなる最初の数は159です。平方根や総和などの記号を二重につけることをゆるすなら、
159 = ( √4 × ( ( Σ(√4) )4) ) - Σ(√4)
Σ(√4) = Σ2 = 3 ですから、それの4乗は81、√4をかけて162、そこからΣ(√4) = 3 を引けば、求めるものになります。次のような解もあります。
159 = 4+ (Σ(Σ4)) + (√( Σ4 ))4
右辺第一項は4です。第二項はΣ10だから55。そして、Σ4 = 10、の平方根を4乗すると(つまり√10を4回、かけあわせると)100です。これらを足すと、4+55+100 でやはり159になります。
すっぴんの4に特殊記号を二重につけることを許可しても、なお作れない数が、0~1000の範囲で3つあります。671 と 797 と 929 です。すっぴんの4に対して三重に特殊記号をつけることをゆるすなら、これらも作れるようになります。
671 = √4 + Σ(√4) + Σ[ { (Σ(√4))! }√4 ]
Σ(√4) は3、その階乗は6、それを√4乗(つまり二乗)して36。で、Σ36 = 666 なので和は671
797 = 4! + Σ(√4 + { (Σ(Σ(Σ4)))) / (√4) }
Σ4=10、ΣΣ4=Σ10=55、ΣΣΣ4=Σ55=1540 なので { } のなかみは770、合計797
929 = 4 + Σ[ { Σ(Σ4) } - { (Σ(√4))! } ] - Σ((4!))
第一項は4。第二項、最初の中かっこは55、2個めの中かっこは6で差は49、それ全体の大きなΣ、つまりΣ49=1225。第三項はΣ24=300。要するに 4+1225-300 = 929
また、671の場合、(すっぴんの4だけじゃなく)二項演算の結果に対しても特殊記号を二重につけて良いとしても、作り方があります。
671 = √4 + Σ(√4) + Σ(Σ( 4+4 ))
この例では、4+4を先に計算して、その結果に総和記号を二重につけてます。Σ8=36、ΣΣ8=Σ36=666だからトータルで671
いずれにせよ、4つの4に対して四則演算と累乗、総和、階乗を適当に組みあわせれば、0~1000のすべての整数を発生させることができます。二項演算の結果のほうに特殊記号を二重、三重につける可能性については、まだ充分に探索してません。二項演算の結果も含めて特殊記号の二重使用だけでは797と929は作れないようです。三重使用まで考えれば、「単項の4だけ」に限って特殊記号を三重につけることで、1000までのすべての数が作れます。
1000までの数で、特殊記号の三重使用なしに作り方が見つからなかったのは797と929です。――なにやら複雑で大変な調査をしたようにも読める書き方かもしれませんが、JavaScriptでは数分でスキャンできます。もっとも、数分でこれだけの式表現空間の深みを正確にスキャンできるような、そういうスクリプトを開発するのには、何日もかかってます。このスクリプトは「4つの4」に限らず、同様のいろいろなパズル一般に適用可能な原理にもとづいています。――
逆に単項の4だけ特殊記号の三重使用を認めると、二項演算の結果には特殊記号を三重どころか二重使用も認めず一重使用しか認めないにもかからず、0~3000の範囲ではほとんどすべての数――少なくとも2940個――が作れます。現在(2002年6月5日)4つの4からの作り方が分かっていない最小の自然数は1937です。1937, 1979, 1985, 1993 の4つを解決すると、2000までのすべての数が4つの4で生成されることになります。単項の4だけの特殊三重でこれなので、もっと広い式表現空間を探索すれば、答があるかもしれません。
特殊記号を何重にも使ったとしても、アルゴリズム的には、まったく同様に検索ができます。具体的にいうと、
four4s(1,1,1,1)
という関数呼び出しにて「特殊記号を一重に使った全表現空間」をスキャンでき、
four4s(2,1,1,1)
なら単項のみ特殊二重、
four4s(3,1,1,1)
なら単項のみ特殊三重、
four4s(2,2,2,2)
なら、あらゆる場所で特殊記号の二重使用を許可。例えば、
four4s(5,5,5,5)
を実行すると、きわめて広い範囲(あらゆる場所で特殊記号を最高5重まで許可)をスキャンできます――が、現状、実行時間が予期できません。100までいければ上等という考えで始めて、最近、捜索範囲を1000まで広げたのですが、それすらも
four4s(3,1,1,1)
でコンプリートできるのですから(そして、このくらいなら、数分程度しかかからない)、
four4s(5,5,5,5)
がものすごい空間であることは想像がつくでしょう。
単項以外の場所の特殊記号の多重使用を認めた場合にあらわれた、鮮烈に印象的な例は、次の表現です。
かっこ内の第一項は三重根号の4、つまり2の4乗根にあたります。第二項 (4(4)1/4)1/2は32の4乗根です。両方とも無理数なのです。このような無理数同士を足し算しても、なお無理数ですが、その和の4乗をとることで162を得ています。かっこ内の和は、162の4乗根だったわけです。いったん複雑な無理数になっても、それを使って初めて問題が解ける場合があるということです。four4s(1,1,1,1)のような範囲だと、小数点がつく数がでたらそのまたルートなんてムダな計算せずにそこで(その方向の捜索は)終わりにしたいというか、終わりにしても良いのですが、あらゆる場所で特殊記号の多重使用を許可した場合には、そうした「ふつう考えられない」ような先にまれに答があるかもしれません。
なお、上の式が実際に162に等しくなることは、高校数学の計算練習といったところです。ちからまかせに解くには
(21/4 + 321/4)4
を二項定理で展開してください。ご存じかもしれませんが、
(a+b)4 = a4 + 4a3b + 6a2b2 + 4a3b + b4
のように係数は1,4,6,4,1です(分からなくなったら1,1から初めて三角形に二項係数を書けば良い)。
4乗の項は明らかに整数になります。そして例えば第二項は
4((21/4)3)(321/4) = 4(23/4)(321/4)
32が2の5乗であることから、321/4=25/4
指数法則から (23/4)(25/4) = 28/4 = 22 = 4
どの項もこんな感じで整数になります。
じつは、これだけ「4つの4で遊ぼうよ」シリーズを続けてきながら、実際にはパズルを1個も解いてません。こころみてきているのは「4つの4を使って与えられた数を作るパズル」を解くことではなく、「4つの4を使って与えられた数を作るパズル」を解くプログラムを作ることでした。パズルを解いていたのでなく、パズルを解くアルゴリズムを解いていたのです。
最初、かなり強引なちからわざで場当たり的、総当たり的に式表現を検索したところ、0から100までの解を得るのに6分くらいかかっていました。今では「とりあえず答がでればいい」というのであれば、0から1000の範囲をもっと短い時間で一気に検索できます。さらに、その数の作り方が何とおりかある場合に、最もシンプルな式を探すアルゴリズムも実装できました。(どの演算がシンプルか、例えば平方根と階乗はどちらがシンプルか、というのは定義しだいですが、基本的にどのような定義にも対応することができます。)
新しいアルゴリズムの考え方については、先日「「4つの4」問題、最終解決のきざし」でメモしましたが、これは読んで分かりやすいメモじゃないです。どのようにすれば簡単に「式の複雑さ」を評価できるのか、そしてより簡単な式表現を選択するようにできるのかも、まだ説明してません。これらについては、後日、詳しく書く予定です。
現時点では、あまり技巧的な高速化をしないで広く動かしていますが、それでも、例えば、特殊記号の二重使用を考えない範囲で0から1000の範囲をスキャンするのは10秒程度です。単にスキャンするだけでなく「最もシンプルな答を求める場合」(式表現の最適化)は2~3倍程度の時間がかかります。部分的に特殊記号の二重使用、三重使用で生成可能な範囲まで検索すると、数分から10分程度かかります。部分的な検索でも、けっこう時間がかかるのです。このあたりについては、現段階では何とも言えません。
「数学パズル「4つの4」入門」のつづきです。前回は問題の雰囲気をざっとつかみました。今回は、パズルを解くための自律的思考アルゴリズムの基礎を紹介します。100行未満の小さなスクリプトでブーツストラッピングが始まり自走していく姿が、かなり印象的です。
すでに見たように例えば「4」を出発点にするとに
4 → √4
4 → 4!
4 → Σ4
といったことで「作れる数の可能性」をふやせます。もちろん「4」が与えられたとき、そのまま何もしない、という選択もあります。
4 → 4
同様に (4+4) というひとつの表現をもとに、
(4+4) → √(4+4)
(4+4) → (4+4)!
(4+4) → Σ(4+4)
(4+4) → (4+4) (何もしない)
の4とおりができます。得られた(√(4+4)) を出発点にすれば、
(√(4+4)) → √(√(4+4))
(√(4+4)) → (√(4+4))!
(√(4+4)) → Σ(√(4+4))
(√(4+4)) → (√(4+4))
がでます。このように、ひとつの項に対して、単項演算子を適用することで「知っている」式表現が増えます。そのうちのいくつかは無効な表現です。上の例ですと、(√(4+4))! や Σ(√(4+4)) は、無効とみなされます。
自分がいま知っているすべての項を把握し、そのひとつひとつにすべてのパターンの単項演算子を適用して自律的に知識を増やす、というスクリプトの骨格を紹介します。まず単項演算子を定義します。ここでは概念を理解するのが目的なので、簡単のため平方根と階乗だけ考え、階乗も3と4に対してのみ値を返すようにしましょう。NOOPは何もしないで入力をそのまま返す演算子です。
var oUnaryOperators = new Object();
oUnaryOperators["NOOP"] = function( n ) {
return n;
}
oUnaryOperators["Math.sqrt"] = function( n ) {
if( n < 0 ) return void 0;
else return Math.sqrt( n );
}
oUnaryOperators["Factorial"] = function( n ) {
if(n==3) return 6;
else if(n==4) return 24;
else return void 0;
}
oUnaryOperators は関数列で、演算子の名前をキーとして関数を値とするハッシュです。これをキーにたばねておくのは、次のようなことをやらかすためです。
function think_about( oExpression_for ) {
var new_brain = new Object();
for( value in oExpression_for ) {
enrich( oExpression_for[value] , value , new_brain );
}
return new_brain;
}
function enrich( proto_expression, proto_value , oExpression_for ) {
for(var op_name in oUnaryOperators) {
var new_value = oUnaryOperators[ op_name ]( proto_value );
if( new_value === void 0 ) continue;
if( op_name === "NOOP" ) {
var new_expression = proto_expression;
} else {
var new_expression = op_name + "( " + proto_expression + " )";
}
if( oExpression_for[ new_value ] === void 0 ) {
oExpression_for[ new_value ] = new_expression;
}
}
}
var knowledge = new Object();
knowledge[ "4" ] = "4";
var new_knowledge = think_about( knowledge );
for( var value in new_knowledge )
document.write( "<p>わたしは" + value + "を意味する記号列" + new_knowledge[value]
+ "を知ってます<\/p>" );
"4" が4を意味することだけ教えてあげると、あとは自分で考えて自分のデータベースを更新します。データベースに入るのは式表現とその式の意味(値)の対であり、値をキーとするハッシュです。出力例:
わたしは4を意味する記号列4を知ってます わたしは2を意味する記号列Math.sqrt( 4 )を知ってます わたしは24を意味する記号列Factorial( 4 )を知ってます
オブジェクト new_knowledge には例えば 24 というプロパティがあって、new_knowledge のプロパティ「24」の値は、Factorial( 4 ) という文字列です。
new_knowledge["24"] = "Factorial( 4 )"
というのは「24」の作り方についての知識(4の階乗)と解釈することも、記号列「Factorial( 4 )」は「24」を意味する、と解釈することもできます。本質的にはプロパティが数値で値が文字列なのですが、JavaScriptの仕様上、プロパティは文字列なので、両方、文字列になってます。キーの文字列は直接、数値を表し、値の文字列はその数値と等しい式表現です。
まったく同じ発想で二項演算子を処理すれば、あとはスクリプトがパズルを自動解決してくれるようになります。上の続き。
var oBinaryOparators = new Object();
oBinaryOparators["+"] = function(x,y) {
return eval(x)+eval(y);
}
oBinaryOparators["-"] = function(x,y) {
return x-y;
}
oBinaryOparators["*"] = function(x,y) {
return x*y;
}
oBinaryOparators["/"] = function(x,y) {
if( y==0 ) return void 0;
else return x/y;
}
function mix( oExpression1_for, oExpression2_for, oNewExpressionsFor ) {
for( var value1 in oExpression1_for ) {
for( var value2 in oExpression2_for ) {
for( var op_name in oBinaryOparators ) {
var new_value = oBinaryOparators[ op_name ]( value1, value2 );
if( new_value === void 0 ) continue;
var expr1 = oExpression1_for[ value1 ];
var expr2 = oExpression2_for[ value2 ];
var new_expression = "(" + expr1 + ")" + op_name + "(" + expr2 + ")" ;
if( oNewExpressionsFor[ new_value ] === void 0 )
oNewExpressionsFor[ new_value ] = new_expression;
}
}
}
}
var expression_for = new Object();
mix( new_knowledge, new_knowledge, expression_for );
for( var value in expression_for )
document.write("<p>わたしは" + expression_for[value] + "が"
+ value + "を意味することを知ってます。<\/p>");
出力例:
わたしは(4)+(4)が8を意味することを知ってます。 わたしは(4)-(4)が0を意味することを知ってます。 わたしは(4)*(4)が16を意味することを知ってます。 わたしは(4)/(4)が1を意味することを知ってます。 わたしは(4)+(Math.sqrt( 4 ))が6を意味することを知ってます。 わたしは(4)-(Math.sqrt( 4 ))が2を意味することを知ってます。 わたしは(4)+(Factorial( 4 ))が28を意味することを知ってます。 わたしは(4)-(Factorial( 4 ))が-20を意味することを知ってます。 わたしは(4)*(Factorial( 4 ))が96を意味することを知ってます。 わたしは(4)/(Factorial( 4 ))が0.16666666666666666を意味することを知ってます。 わたしは(Math.sqrt( 4 ))-(4)が-2を意味することを知ってます。 わたしは(Math.sqrt( 4 ))/(4)が0.5を意味することを知ってます。 わたしは(Math.sqrt( 4 ))+(Math.sqrt( 4 ))が4を意味することを知ってます。 わたしは(Math.sqrt( 4 ))+(Factorial( 4 ))が26を意味することを知ってます。 わたしは(Math.sqrt( 4 ))-(Factorial( 4 ))が-22を意味することを知ってます。 わたしは(Math.sqrt( 4 ))*(Factorial( 4 ))が48を意味することを知ってます。 わたしは(Math.sqrt( 4 ))/(Factorial( 4 ))が0.08333333333333333を意味することを知ってます。 わたしは(Factorial( 4 ))-(4)が20を意味することを知ってます。 わたしは(Factorial( 4 ))-(Math.sqrt( 4 ))が22を意味することを知ってます。 わたしは(Factorial( 4 ))/(Math.sqrt( 4 ))が12を意味することを知ってます。 わたしは(Factorial( 4 ))*(Factorial( 4 ))が576を意味することを知ってます。
これらのリストは説明のための概念的なものであり、現実の実装には適しません。実装上の詳しい説明は次回以降にまわして、とりあえずパズルをざっと解くための指示を書いてしまいます。上の2つの関数を組み合わせて4つの4で作れるものをデータベースにつっこみ、あとからほしいものを検索するだけです。
var eva = new Array();
for(var i=1; i<=4; i++) eva[i] = new Object();
var oBuffer = new Object();
oBuffer["4"] = "4";
eva[1] = think_about( oBuffer );
var oBuffer = new Object();
mix( eva[1], eva[1], oBuffer );
eva[2] = think_about( oBuffer );
var oBuffer = new Object();
mix( eva[1], eva[2], oBuffer );
mix( eva[2], eva[1], oBuffer );
eva[3] = think_about( oBuffer );
var oBuffer = new Object();
mix( eva[1], eva[3], oBuffer );
mix( eva[2], eva[2], oBuffer );
mix( eva[3], eva[1], oBuffer );
eva[4] = think_about( oBuffer );
for(var i=0; i<=100; i++) {
var expression = eva[4][i.toString()];
if( expression !== void 0 )
document.write( "<p>" + i + " == " + expression + "<\/p>\n");
else
document.write( "<p>" + i + ": 未解決<\/p>\n" );
}
出力例:
0 == (4)+((4)-((4)+(4))) 1 == (4)/((4)+((4)-(4))) 2 == (4)*((4)/((4)+(4))) 3 == (4)-((4)/(Math.sqrt( (4)*(4) ))) 4 == Math.sqrt( (4)+((4)+((4)+(4))) ) 5 == (4)+((4)/(Math.sqrt( (4)*(4) ))) 6 == Math.sqrt( (4)+((4)*((4)+(4))) ) 7 == (4)+((4)-((4)/(4)))
以下100まででます。ここで、eva[1] には1つの4で作れるすべての表現、eva[2] には2つの4で作れるすべての表現、……、eva[4]には4つの4で作れるすべての表現が格納されることに注意してください。ただし「すべて」の意味は、ここで定義した式表現空間の範囲のすべて、です。例えば、44や444を使ったり、指数を使ったり、総和を使ったり、特殊記号を二重に使う方法は、ここでは取り入れてません。上記の動作原理さえ分かれば、そういった細部も簡単に実装できます。
上の出力のかわりに、次のデバッグ用出力を実行すると理解に役立つかもしれません。
function dump( x ) {
for( var value in eva[x] )
document.write("<p>学習プロセス" + x + "において、"
+ value + "を意味する記号列" + eva[x][value] + "を見つけました。<\/p>")
}
dump(1);
dump(2);
dump(3);
dump(4);
出力例の最初の部分です。
学習プロセス1において、4を意味する記号列4を見つけました。 学習プロセス1において、2を意味する記号列Math.sqrt( 4 )を見つけました。 学習プロセス1において、24を意味する記号列Factorial( 4 )を見つけました。 学習プロセス2において、8を意味する記号列(4)+(4)を見つけました。 学習プロセス2において、2.8284271247461903を意味する記号列Math.sqrt( (4)+(4) )を見つけました。 学習プロセス2において、0を意味する記号列(4)-(4)を見つけました。 学習プロセス2において、16を意味する記号列(4)*(4)を見つけました。
以上で「4つの4」パズルをとく自律的思考アルゴリズムの基礎を終わります。次回以降は、計算時間の最適化(高速化)、そして、重要な話題として、ある数を作る方法が2とおり以上ある場合に、より簡潔なほうを選ぶためのアルゴリズム(式表現の最適化)について書く予定です。
「4つの4」パズルを解くアルゴリズム。前回は新しいアルゴリズムの基礎となる考え方を具体的に説明しました。今回は「自律的思考」と名づけたこのアルゴリズムの強力さを、実演してみます。
今回の方法は速度重視(速度面での最適化)であり、4つの4を使った0~1000までの数の作り方が、手元の環境では10秒以内(最短5秒程度)でリストアップされます。 これまでで最も高速だった「ラムダ関数バージョン」ですら、100や200までのリストを作るには1分くらいかかりました。当初は100までのリストを得るのに6分以上かかっていたのです。それが1000まで10秒以下になったのだから、大きな進歩と言うべきでしょう。(いちばん初めは0~30までの作り方だけで10秒くらいかかってたよ。)
なお、「2000以下に4つの4を使っての作り方が分からない数が数個ある」と先日、書きましたが、それも解決しました。0から2000までの数は、すべて4つの4を使って(前回までに定義した範囲内で)表現できます。
前回、説明したようにして、階乗や総和も実装します。あらゆる可能な式表現を検索対象にしたとしても、たかだか有限時間で終了するので数学的には「解けた」ということになりますが、人間の時間で考えると、手元のパソコンでせいぜい数分くらいで答が出てほしいでしょう。
そのための基本的な手段は、捜索範囲を制限することです。
第一の制限は、論理的に無意味な(あるいは、ほとんど無意味な)範囲の切り捨て。例えば、マイナスの数は捜索範囲から外してかまいません。計算の途中でマイナスの数が出てきて最終的にプラスになることもありえますが、マイナスの数を経由して作れる数は、必ずマイナスの数を経由しなくても作れるので、結局、マイナスの数は考えなくて良いです。また、例えば「√2乗」のような、無理数乗の計算も、最終的に整数を作るというパズルの目的のうえでは、まったく無意味と言っていいでしょう。
第二の制限は、速くするための制限。例えば、1000までの数を作る場合において、途中で2000より大きくなったら、その方向は捨ててしまってもかまいません。実際には、いったん2000より大きい数を経由してから、エレガントに目的の数にたどりつくような計算法もありえます。しかし、答がきれいでなくても、とにかく計算が合えばいい、という速度重視の立場からは、なるべく少ない材料でやりくりしたほうがトクです。同じ理由から、途中で小数が発生したら、それは捨ててかまいません。整数の組み合わせだけで1000までの数をぜんぶ作れるからです。
例えば次のようになります。
function isInt( n ) {
return ( n - Math.floor(n) == 0 );
}
var new_value = oUnaryOperators[ op_name ]( proto_value );
if( new_value === void 0 ) continue;
if( new_value < 0 || new_value > TOO_BIG || !isInt(new_value)) continue;
単項演算子、二項演算子も、範囲外の数が来たらまじめに計算しないでただちにvoid 0を返して計算をうち切ります。このことによって――特に小数をいっさい使わないようにすることによって――驚異的なスピードアップが図れます。小数の端数がつく数も考慮した場合に数分ないし数十分以上かかるものが、整数だけでやると10秒以内でできるようになります。もっとも得られるパズルの解は最もシンプルなものとは限りません。例えば、
10 = Σ( 4+4×(4-4) )
などという変てこな出力が出るかもしれません。計算は合ってますが、そんな面倒なことしなくても、
10 = (44-4)/4
のほうが、シンプルで「良い」答でしょう。どうしたら最もシンプルな解答ができるか――つまりどうしたら式表現を最適化できるか――は、べつの問題であり、次回以降に説明します。解答速度を高速化することと、式の美しさを最適化することとはトレードオフの関係にあり、なんでもいいからとにかく速く答を見つける、ということは、考え得るすべての式表現のなかでいちばんきれいなものを見つける、ということとは、異なる方向性にあります。
var oBuffer = new Object();
oBuffer["44"] = "44";
mix( eva1, eva1, oBuffer , 2 );
var eva2 = think_about( oBuffer , 2 );
前に eva[1], eva[2] , ... とオブジェクトの配列で書きましたが、この書き方だとIEが異様に遅くなるようなので、上のようにベタの eva1, eva2, ... に書き換えました。本当は配列で書いておくほうがあとで簡単化しやすいのですが、まぁ、意味は同じことです。